Binary Entropy Vectors
Characterizing the set of entropy vectors under various distribution constraints is a fundamentally important problem in information theory [B1, B2]. Not only would such an accurate characterization allow for the determination of all information inequalities, but it would enable the direct computation of all rate regions for network coding and multiterminal source coding. That is, understanding the fundamental limits for communication over networks is inherently linked with understanding the boundary of the set of entropic vectors.
The interest in the (closure of) the set of entropy vectors for discrete unbounded cardinality random variables N* [B1] and its normalized counterpart N* [B2, B3] originated in the study of linear information inequalities [B4, B5, B6], as these correspond to supporting halfspaces for these sets. More recently, it has been noted that the network coding capacity region [B1, B7] is a linear projection of N* intersected with a vector subspace. These two problems are inherently related, as it has been shown [B8] that for every non-Shannon type inequality (i.e., every supporting half space of N*) there is a multi-source network coding problem for which the capacity region requires this inequality.
More generally, as all achievable rate regions in information theory are expressed
in terms of information measures between random variables obeying certain
distribution constraints, they can be expressed as linear projections of entropy
vectors associated with these constrained random variables. Hence, there is a
fundamental interest in multi-terminal information theory in the region of entropy
vectors N*(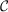 ) associated with random variables obeying distribution constraints
) associated with random variables obeying distribution constraints
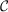 .
.
N* is difficult to characterize for arbitrary N ≥ 4, as Mat¨š recently
definitively proved [B9], because there are an infinite number of associated linear
information inequalities. There are few known computationally tractable inner
bounds for N* for N ≥ 4 [B10] [B3], and it is generally unknown how to
determine whether a given candidate vector h ∈ R+2N-1
is entropic or not. A
computational algorithm capable of determining whether or not h ∈N*
is not presently available for N ≥ 4. Our work [A1, A2] points out that
by restricting the discrete random variables to be binary, one can obtain
efficient descriptions of the entropy region, called the set of binary entropy
vectors, ΦN. In particular, we introduce an algorithm which can definitively
determine whether a candidate vector h ∈ R+2N-1
can be generated by a
distribution on N bits. This has enabled us to deliver in [A3, A4, A2] our
primary contribution: an algorithm which, given any polytope outer bound for
convΦN(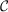 ), returns a tuned inner bound agreeing on all of its (tight) exposed faces
shared with convΦN(
), returns a tuned inner bound agreeing on all of its (tight) exposed faces
shared with convΦN(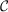 ). Because the inner bounds have this property, their
performance increases with increasingly better performing outer bounds. The inner
bound technique is easily extended to obtaining bounds for convN*(
). Because the inner bounds have this property, their
performance increases with increasingly better performing outer bounds. The inner
bound technique is easily extended to obtaining bounds for convN*(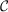 ) and
convN*(
) and
convN*(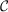 ) as a function of outer bounds for these sets, as they contain
convΦN(
) as a function of outer bounds for these sets, as they contain
convΦN(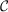 ).
).
Our current work is applying these inner bound techniques to gain insights about the tightness of existing outer bounds for N*, and is dedicated to finding as many extreme points of N* as possible.

Fig. 1: Pictorial representation of relationships among bounds for the region of normalized entropy vector 4* that are discussed in [A3, A4, A2].
Funding for this Topic:
 This work supported by the National Science Foundation under the CAREER
award CCF-1053702.
This work supported by the National Science Foundation under the CAREER
award CCF-1053702.
Relevant Publications & Presentations
[A1] John MacLaren Walsh and Steven Weber, “A Recursive Construction of the Set of Binary Entropy Vectors,” in Forty-Seventh Annual Allerton Conference on Communication, Control, and Computing, Sept. 2009, pp. 545–552. [Online]. Available: http://www.ece.drexel.edu/walsh/binEntSetConf-v5-JW.pdf
[A2] J. M. Walsh and S. Weber, “A Recursive Construction of the Set of Binary Entropy Vectors and Related Inner Bounds for the Entropy Region,” IEEE Trans. Inform. Theory, Oct. 2011, scheduled to appear.
[A3] John MacLaren Walsh and Steven Weber, “Tunable Inner Bounds for the Region of Entropy Vectors,” Feb. 2010, 2010 Information Theory and Applications Workshop, University of California San Diego. [Online]. Available: http://www.ece.drexel.edu/walsh/walshITA10.pdf
[A4] ——, “Relationships Among Bounds for the Region of Entropic Vectors in Four Variables,” in 2010 Allerton Conference on Communication, Control, and Computing, Sept. 2010. [Online]. Available: http://www.ece.drexel.edu/walsh/allerton10.pdf
[A5] ——, “An Inner Bound Technique on the Normalized Set of Entropy Vectors,” Sept. 2009, DARPA ITMANET Meeting, MIT. [Online]. Available: http://www.ece.drexel.edu/walsh/weberITMANET0909.pdf
[A6] ——, “Properties of the Binary Entropy Vector Region,” Mar. 2009, DARPA ITMANET Meeting, Stanford University. [Online]. Available: http://www.ece.drexel.edu/walsh/weberITMANET0309.pdf
[A7] John MacLaren Walsh, Steven Weber, Drakontas LLC, “Optimal Coded Information Network Design and Management via Improved Characterizations of the Binary Entropy Function,” Feb. 2009, Air Force Office of Scientific Research Complex Network Program Review. [Online]. Available: http://www.ece.drexel.edu/walsh/walshAFOSR09.pdf
External References
[B1] Raymond W. Yeung, Information Theory and Network Coding. Springer, 2008.
[B2] B. Hassibi and S. Shadbakht, “Normalized Entropy Vectors, Network Information Theory and Convex Optimization,” in IEEE Information Theory Workshop on Information Theory for Wireless Networks, July 2007, pp. 1 – 5.
[B3] ——, “On a Construction of Entropic Vectors Using Lattice-Generated Distributions,” in IEEE International Symposium on Information Theory (ISIT), June 2007, pp. 501 – 505.
[B4] Zhen Zhang and Raymond W. Yeung, “A Non-Shannon-Type Conditional Inequality of Information Quantities,” IEEE Transactions on Information Theory, vol. 43, no. 6, Nov. 1997.
[B5] ——, “On Characterization of Entropy Function via Information Inequalities,” IEEE Transactions on Information Theory, vol. 44, no. 4, July 1998.
[B6] R. Dougherty, C. Freiling, and K. Zeger, “Networks, Matroids, and Non-Shannon Information Inequalities,” IEEE Transactions on Information Theory, vol. 53, no. 6, pp. 1949–1969, June 2007.
[B7] Xijin Yan, Raymond W. Yeung, and Zhen Zhang, “The Capacity Region for Multi-source Multi-sink Network Coding,” in IEEE International Symposium on Information Theory (ISIT), June 2007, pp. 116 – 120.
[B8] T. Chan and A. Grant, “Entropy Vectors and Network Codes,” in IEEE International Symposium on Information Theory, June 2007.
[B9] František Mat˙š, “Infinitely Many Information Inequalities,” in IEEE International Symposium on Information Theory (ISIT), June 2007, pp. 41–44.
[B10] T. Chan and R. Yeung, “On a relation between information inequalities and group theory,” IEEE Transactions on Information Theory, vol. 48, no. 7, pp. 1992 – 1995, July 2002.
